GitHub

KitML and scientific machine learning

Machine learning is building its momentum in scientific computing. Given the nonlinear structure of differential and integral equations, it is promising to incorporate the universal function approximator from machine learning models into the governing equations and achieve the balance between efficiency and accuracy. KitML is designed as a scientific machine learning toolbox, which devotes to fusing mechanical and neural models. For example, the Boltzmann collision operator can be divided into a combination of relaxation model and neural network, i.e. the so-called universal Boltzmann equation.

\[\frac{df}{dt} = \int_{\mathcal{R}^{3}} \int_{\mathcal{S}^{2}} \mathcal{B}(\cos \beta, g)\left[f\left(\mathbf{u}^{\prime}\right) f\left(\mathbf{u}_{*}^{\prime}\right)-f(\mathbf{u}) f\left(\mathbf{u}_{*}\right)\right] d \mathbf{\Omega} d \mathbf{u}_{*} \simeq \nu(\mathcal{M}-f)+\mathrm{NN}_{\theta}(\mathcal{M}-f)\]

The UBE has the following benefits. First, it automatically ensures the asymptotic limits. Let's consider the Chapman-Enskog method for solving Boltzmann equation, where the distribution function is approximated with expansion series.

\[f \simeq f^{(0)}+f^{(1)}+f^{(2)}+\cdots, \quad f^{(0)}=\mathcal{M}\]

Take the zeroth order truncation, and consider an illustrative multi-layer perceptron.

\[\mathrm{NN}_{\theta}(x)=\operatorname{layer}_{n}\left(\ldots \text { layer }_{2}\left({\sigma}\left(\text { layer }_{1}(x)\right)\right)\right), \quad \operatorname{layer}(x)=w x\]

Given the zero input from $M − f$, the contribution from collision term is absent, and the moment equation naturally leads to the Euler equations.

\[\frac{\partial}{\partial t}\left(\begin{array}{c} \rho \\ \rho \mathbf{U} \\ \rho E \end{array}\right)+\nabla_{\mathbf{x}} \cdot\left(\begin{array}{c} \rho \mathbf{U} \\ \rho \mathbf{U} \otimes \mathbf{U} \\ \mathbf{U}(\rho E+p) \end{array}\right)=\int\left(\begin{array}{c} 1 \\ \mathbf{u} \\ \frac{1}{2} \mathbf{u}^{2} \end{array}\right)\left(\mathcal{M}_{t}+\mathbf{u} \cdot \nabla_{\mathbf{x}} \mathcal{M}\right) d \mathbf{u}=0\]

KitML provides two functions to construct universal Boltzmann equation, and it works seamlessly with any modern ODE solver in DifferentialEquations.jl.

KitML.ube_dfdt — Function
ube_dfdt(f, p, t)

Right-hand side of universal Boltzmann equation

Arguments

  • $f$: particle distribution function in 1D formulation
  • $p$: M, τ, ann (network & parameters)
  • $t$: time span
source
KitML.ube_dfdt! — Function
ube_dfdt!(df, f, p, t)

Right-hand side of universal Boltzmann equation

Arguments

  • $df$: derivatives of particle distribution function
  • $f$: particle distribution function in 1D formulation
  • $p$: M, τ, ann (network & parameters)
  • $t$: time span
source

Besides, we provide an input convex neural network (ICNN) developed by Amos et al.

The neural network parameters are constrained such that the output of the network is a convex function of the inputs. The structure of the ICNN is shown as follows, and it allows for efficient inference via optimization over some inputs to the network given others, and can be applied to settings including structured prediction, data imputation, reinforcement learning, and others. It is important for entropy-based modelling, since the minimization principle works exclusively with convex function.

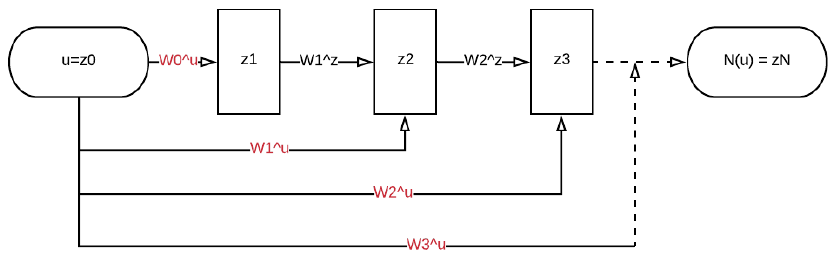
Solaris.Convex — Type
struct Convex{T1<:AbstractArray, T2<:Union{Flux.Zeros, AbstractVector}, T3} <: Solaris.AbstractLayer

Input Convex Neural Network (ICNN) layer by Amos et al.

source

Besides, we also provide scientific machine learning training interfaces and I/O methods. They are consistent with both Flux.jl and DiffEqFlux.jl ecosystem.

Solaris.sci_train — Function
sci_train(ann, data)
sci_train(ann, data, θ)
sci_train(
    ann,
    data,
    θ,
    opt,
    args;
    device,
    iters,
    ad,
    kwargs...
)

Scientific machine learning trainer

Arguments

  • $ann$: neural network model
  • $data$: dataset
  • $θ$: parameters of neural network
  • $opt$: optimizer
  • $ad$: automatical differentiation type
  • $args$: rest arguments
  • $device$: cpu / gpu
  • $iters$: maximal iteration number
  • $kwargs$: keyword arguments
source
sci_train(loss, θ)
sci_train(
    loss,
    θ,
    opt,
    args;
    lower_bounds,
    upper_bounds,
    cb,
    callback,
    iters,
    ad,
    epochs,
    kwargs...
)
source
Solaris.sci_train! — Function
sci_train!(ann, data)
sci_train!(ann, data, opt; device, epoch, batch)

Scientific machine learning trainer

Arguments

  • $ann$: neural network model
  • $data$: tuple (X, Y) of dataset
  • $opt$: optimizer
  • $epoch$: epoch number
  • $batch$: batch size
  • $device$: cpu / gpu
source
sci_train!(ann, dl)
sci_train!(ann, dl, opt; device, epoch)
source
sci_train!(ann, data; device, split, epoch, batch, verbose)

Trainer for Tensorflow model

source